
Background: J.D. Drew hit a monster home run during the 1997 season, but it hit a tree in flight (while still 85' off the ground) so the length of the homer could not be determined. After reading an article in the newspaper (2/04/1997 Tallahassee Democrat) about this problem, including some estimates by the coaches and a request for some help ("Now there's a science problem for you," FSU coach Mike Martin said. "We ought to get one of our science professors over to calculate how far that might have gone."), I stopped by practice to find out more and see if I could help. The two letters to Coach Martin included below were the result.
The first letter gives relevant data obtained from a conversation with the coach and a first estimate, while the second letter gives a summary of my numerical findings. The numerical model in my program is based on the equations and tabulated drag coefficients in ``The Physics of Baseball'' by Robert K. Adair.

Coach Mike Martin
Moore Athletic Center
FSU Campus 4043
Dated: February 5, 1997
Dear Coach Martin:
I thought it would be useful to summarize my conclusions about the length of the home run J.D. Drew hit last weekend, stating the facts as I know them at this time and an estimate of the distance the ball would have traveled. As I told you on the field yesterday, a conservative estimate puts the home run at about 500'. It could be longer, but I need to do some calculations as described below to estimate the effect of a following wind and a lower trajectory.
The one number that I consider reliable is the distance to the fence where the ball went out. You told me 325', and this is consistent with what I would expect for a point about 2/3 of the way between the the line (307') and the light tower (339'). I paced off the distance from the wall to under the top of the tree as being about 100'. It will be convenient to use 430' for the total distance to the tree. I agree with the estimate that the ball hit the tree about 80' to 90' up. Improving the accuracy of these numbers would help some, but the answer will always be uncertain.
My estimate of where the ball would have landed is obtained from a graph in ``The Physics of Baseball'' by Robert Adair. His calculations have some absolute uncertainty (that is, the speed required for a particular trajectory might be wrong), but the key thing we need is the shape -- the curvature -- of the trajectory on its downward flight. This is probably quite good for our purposes, but his graph does assume the ball was hit at the optimum angle of 35 degrees.
We can use Adair's graph to bracket where the ball would land based on the numbers above. An upper limit would be if the ball was 90' high at 435' from the plate; it would land about 510' away. This ball would have left the bat at 130 mph. A lower limit would be if the ball was 80' high at 425' away; it would land about 490' out, having left the bat at about 125 mph. Either would have been in level flight and about 130' high when going over the fence.
Based on comments in the paper and from a maintenance man I talked to, it seems likely that the ball was hit on a lower trajectory and therefore much harder, which is reasonable since an aluminum bat was used. The weather forecast suggests there might have been as much as a 10 mph following breeze, which also helps the ball carry. These would, I believe, increase the distance to the final landing point, but to quantify this I will have to put together a program to repeat the calculations Adair did. I will let you know what I learn. In the meantime, I think it is safe to say that the ball would have traveled at least 500', and possibly more.
By the way, descriptions of Reggie Griggs' home run suggest it was close to 500' if it did hit in that old oak tree. If it was hit higher in the air than J.D.'s ball, that would suggest a flatter and longer trajectory for Drew's homerun than this initial estimate.
Thanks for taking the time to talk to me during practice.
Sincerely, ...

Coach Mike Martin
Moore Athletic Center
FSU Campus 4043
Dated: February 7, 1997
Dear Coach Martin:
As I wrote in my previous letter concering an estimate of the actual length of J.D. Drew's home run last weekend against UNC-Asheville, if the ball was hit on a lower trajectory -- that is, more of a line drive than a fly ball -- it would travel further than the minimum distance of 500' I estimated from a graph in ``The Physics of Baseball'' by Robert Adair. In order to say more, it was necessary to assemble a computer program that did the same calculation shown in Adair's book. That has now been done, and my results appear to be the same within the accuracy of the graphs included in the book. As a reminder, relative effects (like the downward trajectory of a hit ball) are the most reliable predictions of such a model.
I attach a graph that shows a variety of trajectories that (except for a 400' fly ball included for comparison) all go through the same point on the tree, 85' up and 430' away from home plate. The solid curve is the 500' fly ball described in the last letter. The longest shot, landing over 550' away, is possible if the ball is hit very hard, almost 10 % harder than the 500' fly ball, on a much lower trajectory. It barely gets over 100' in the air and would have been still rising as it went over the fence. The curves inbetween are at an intermediate angle, one showing the effect of a following wind.
In conclusion, Drew's home run was probably in the 520' to 550' range and could have been longer. Comparison of these curves to what various witnesses saw should allow you to get a better estimate of how long it was. For example, if it never got much higher that a 400' batting practice shot that hits in the street out there, Drew's home run would have been in the 550' territory.
Give my regards to J.D.
Sincerely, ...

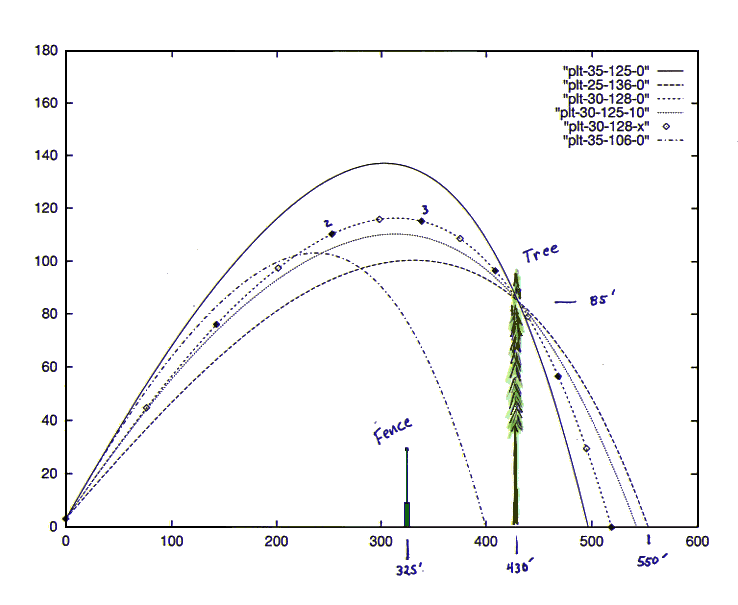
The legend in the upper corner (from gnuplot) will be relocated when I get a chance to clean up the drawing. The solid curve is on the optimal 35 degree trajectory, launched at 125 mph. The longest ball was hit at 136 mph at 25 degrees. They were in flight for about 6 seconds, as the half-second marks show.

It should be obvious that I did not include any technical remarks in my letter to Coach Martin, for obvious reasons. You may note that I did document my assumptions about the data upon which the calculational estimates are based, but not much else.
I intend to explain more about the calculation and include some relevant tables here ....