These diagrams were made to illustrate the intial steps in the solution to a problem where a spinning ball is placed on a surface so that friction supplies a torque that slows the rotation and a force that makes the ball translate. [It can equally well apply to a situation where a ball is thrown so it is initially not rotating, and friction provides the torque that makes the ball rotate and a force that slows its translation.]
A standard force diagram is shown below. It corresponds to the case where the ball was initially rotating in a clockwise sense (angular velocity points "into the board"). [The ball is moving to the left in the equivalent problem.]
Note:
I omit the force of gravity (down) and the contact force (up)
for clarity because they sum to zero and produce no net force
or torque in this problem.
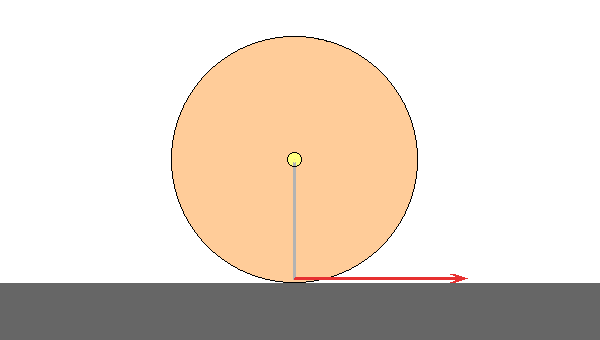
Because the surface of the ball is moving to the left relative to the surface, the friction force (shown with the red arrow) is to the right. I will ignore the details of calculating this force, since the issue here has to do with identifying the forces and torques that act on the body.
The force analysis of this diagram says there is a net force to the right due to the one (red) force shown, and this will make the ball accelerate to the right. [In the equivalent problem, this force slows the ball's translation.]
Because the red force acts at the edge of the ball, it applies a torque about the center of the ball. It is the only torque in the problem. The lever arm is shown as a very light gray line. The right-hand-rule tells us that this torque is in the counter-clockwise sense, with the torque vector pointing "out of the board". This torque will slow the rotation of the ball. [In the equivalent problem, the torque causes the ball to start to rotate in the counter-clockwise sense.]
Together the net force and net torque tell us how to calculate the linear and angular acceleration quantitatively if we know the amount of friction present and the mass and moment of inertia of the ball.
There is an alternative way of diagraming this problem that introduces some extra forces that do not change the physics in any way but allow you to group the forces into separate sources of a pure force and a pure torque. Some find this conceptually simpler than using a single force to produce both the force and the torque.
I reiterate that the problem remains the same. This is the physics equivalent of adding zero to an equation, and then replacing "0" with "(-1) + (+1)" as a conceptual aid in doing certain algebraic manipulations that could just as well be done some other way.
A diagram of this is shown below, where we have added zero force and zero torque to the diagram by adding the forces shown with blue and green arrows. Because these two forces are equal and opposite, they add zero net force to the problem. Because these two forces act at the same point and along the same line, they also add zero net torque to the problem. We have not changed anything. Note that each of these forces is equal in magnitude to the original (red) force.
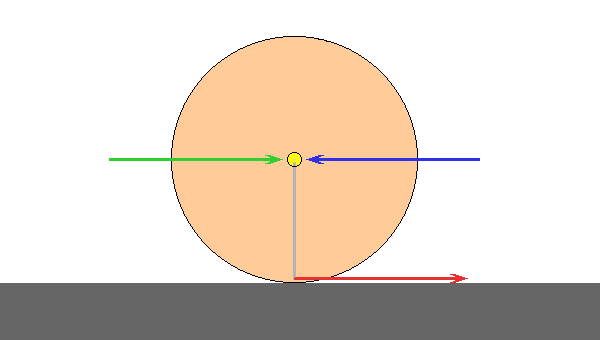
Notice that we have applied these two forces at the center of the ball. This is not by accident, because our next step is to "regroup" the forces, pairing the blue one with the red one.
What we have now is a pair of forces (blue and red) that form what is called a "couple". The red and blue forces are equal and opposite, so these two forces sum to zero. However, since these two do not act at the same point, together they produce a net torque which we will calculate about the center of the ball as before. This pair of forces gives a pure torque which is the only torque present (and thus equal to the net torque), and contribute nothing to the net force. The torque from this "couple" is used to determine the change in angular velocity about the center of mass of the ball. (Notice that the torque due to this "couple" is the same as what we calculated by using the first method up above.)
We have one force (the green one) left over. The green force acts at the center of the ball, so it produces zero torque about that point. Thus this represents a pure force which is equal to the net force, and thus makes the only contribution to the change in the linear velocity of the center of mass of the ball. (Notice that this force is equal to the net force we used in the first method up above.)
What this analysis does is set things up so one group of forces can be treated as the sole source of the net torque about the center of mass, contributing nothing to the net force, and another force can be treated as the sole source of the net force on the center of mass, contributing nothing to the net torque. Some find this conceptually simpler than using one force for two seemingly different purposes.
Note that this kind of analysis is easily extended to cases with more than one force acting at different places, but that you always arrange things so that you end up with a single "pure force" acting at the center of mass plus some number of "couples" that each contribute to the net torque. I think the first method above is the easiest to apply in general, but you might find this second method helpful in seeing why the first method works.
Created by Jim Carr