|Intro| - |Sizes| - |Tour| - |Help|
1 fm (femto meter) = 10^{-15} m = 10-15 m = 0.000000000000001 meters.
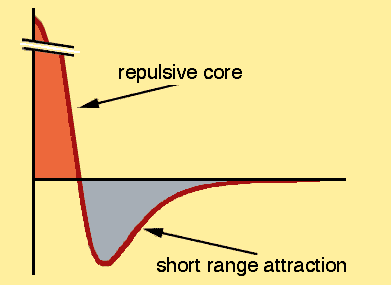
The qualitative features of the nucleon-nucleon force are shown below.

There is an extremely strong short-range repulsion that pushes protons and neutrons apart before they can get close enough to touch. (This is shown in orange.) This repulsion can be understood to arise because the quarks in individual nucleons are forbidden to be in the same area by the Pauli exclusion principle.
There is a medium-range attraction (pulling the neutrons and protons together) that is strongest for separations of about 1 fm. (This is shown in gray.) This attraction can be understood to arise from the exchange of quarks between the nucleons, something that looks a lot like the exchange of a pion when the separation is large.
The density of nuclei is limited by the short range repulsion. The maximum size of nuclei is limited by the fact that the attractive force dies away extremely quickly (exponentially) when nucleons are more than a few fm apart.
Elements beyond uranium (which has 92 protons), particularly the trans-fermium elements (with more than 100 protons), tend to be unstable to fission or alpha decay because the Coulomb repulsion between protons falls off much more slowly than the nuclear attraction. This means that each proton sees a repulsion from every other proton but only feels an attractive force from the few neutrons and protons that are nearby -- even if there is a large excess of neutrons.
Some "superheavy nuclei" (new elements with about 114 protons) might turn out to be stable as a result of the same kind of quantum mechanical shell-closure that makes noble gases very stable chemically.
The following material is more technical and assumes some additional physics knowledge.
The force is more complicated than the cartoon above suggests, however. For example, a common question students ask is "If a proton and neutron form a bound state (deuterium, or 2H), why can't two neutrons form a bound state?"
This is a good question.
If the nuclear force were a simple central force (like gravity) that only depended on distance like shown above, we would expect the di-neutron to be stable just like 2H because neither has any Coulomb repulsion to deal with. (The two protons that would make up 2He would be pushed apart because like charges repel.)
The answer is that the measured properties of the nucleon-nucleon interaction depend on many things, including the kind of particle and spin orientation, and is not strongly attractive under all possible situations. To say more than this requires going into more technical detail than I would like to, so what follows may not be easy to follow on the first reading.
There are four different ways that a pair of protons and/or neutrons can be combined, and the force is different in each case. A potential energy graph for each of these, taken from an actual NN interaction used in nuclear physics research, is shown below.
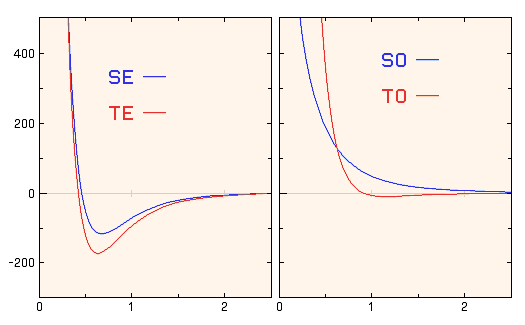
Radial dependence of the `even' part of the NN interaction:
The "even" part of the nucleon-nucleon interaction is shown on the left. This is the part of the interaction that applies when the relative wavefunction is even (symmetric) under exchange of two particles. Notice that it is attractive as described above, with a short range repulsion.
The red curve on the left that is labeled TE is the Triplet-Even (S=1, T=0) case that applies to the deuteron (neutron and proton with parallel spins) in its J=1+ ground state. It is just barely negative enough to bind a neutron and proton into a stable nucleus. Two neutrons cannot be in this configuration because it would violate the Pauli principle for identical particles.
The blue curve on the left that is labeled SE is the Singlet-Even (S=0 T=1) case that applies to the deuteron (as well as the di-neutron or di-proton) with anti-parallel spins (in a J=0+ state). You can see that it is not as negative as the TE interaction, and this small difference is enough that it cannot produce a bound state.
There is another difference, due to the Tensor force, a somewhat longer range interaction predicted by pion exchange, which brings some additional attraction to the J=1 case. Thus this even potential is the main thing that holds nuclei together, but it is not quite enough to bind two neutrons.
Radial dependence of the `odd' part of the NN force:
The "odd" part of the nucleon-nucleon interaction is shown on the right. This is the part of the force that applies when the relative wavefunction is odd (anti-symmetric) under exchange of the radial wave function. Notice that it these basically consists of only the short-range repulsion.
The blue curve on the right labeled SO shows the Singlet-Odd (S=0 T=0) part that applies to an L=1 (P state) of the n-p system with anti-parallel spins.
The red curve on the right labeled TO shows the Triplet-Odd (S=1, T=1) part that applies to nn and pp states with parallel spins. States of this type are not favored in nuclei; they appear at higher energy than the even states, other things being equal.
Simple models:
One of the early models for the NN interaction is known as the Serber force after its inventer (Robert Serber). It includes the qualitative features shown above but used a simple square well potential for the attractive part and also had a repulsive core. It set TE=SE with both repulsion and attraction, and set SO=TO with only the repulsive part for those parts of the force. By fitting just the radius of the repulsion and the range and depth of the attraction, you can explain most of the qualitative features of the NN interaction over a wide range of energies. You only miss on details, including ones like whether the di-neutron is bound.
Quark-model description of nuclear force: