Back to the Overview.

1. Introduction to Drag Forces

Aerodynamic drag forces depend on the size and shape of the object, the density and viscosity of the fluid medium, and the speed of the fluid flow around the object. The standard approach [1] is to make explicit some of the dependences on these variables and hide the rest in an empirical drag coefficient. (This study will completely ignore the Magnus Effect, the cause of sideways forces associated with rotation of the moving body which are essential for a proper treatment of the flight of a baseball.)

The drag force is always in the direction opposite to the velocity (that is, $- {\hat v}$) and has a magnitude given by

$$\left\vert F_{\rm drag} \right\vert \; = \; C_D(Re) \; \frac{1}{2} \rho L^2 \; v^2 .$$ (1)

Here $\rho$ is the density of the medium, L is a ``typical dimension'' of the object being considered, and C_D is the drag coefficient of that object as a function of the Reynolds number, Re. One should also note that the velocity v is defined relative to the rest frame of the medium, which is the frame we use for all of the analyses in this article. More care is needed if there are windage effects to be considered. Two standard graphs of measured values for C_D are included in Section 1.A.

Jump to Section 1.A:
Tables and graphs of standard data

What value of L you use is defined by the convention adopted for the measured values of C_D. For example, the area L² might be $\pi R^2$ for a sphere or disk. Operationally, one measures F_drag for a given set of parameters and deduces the value of C_D by using this formula with a specific definition of L. You must know what definition was used when C_D was determined in order to use some graphed or tabulated data in the formula.

The Reynolds number is a dimensionless parameter defined by

$$Re \; = \; \frac{L v}{\nu} \; = \; \frac{\rho L v}{\eta}$$

where $\nu$ is the ``kinematic viscosity'' and $\eta$ = $\rho \nu$ is the viscosity of the fluid medium. Some typical values for the viscosity are tabulated in Section 1.A. The point of using the Reynolds number in Eq. (1) is that the drag coefficient for a particular shape is the same for different fluids as long as this ratio remains constant. This scaling allows you to relate data for experiments done with different fluids and objects of different size to one another.

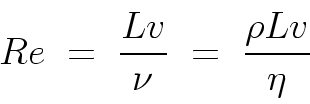
Our parameterization

For our purposes it will be convenient to isolate the dependence of the drag force on one dynamical parameter, the velocity v. For a particular fluid medium (assumed to have a density and viscosity that does not depend on position, a condition violated if the problem extends over a large range of altitudes in the atmosphere) and an object of fixed size and shape, we will define

$$K(v) \; = \; C_D(Re) \; \frac{1}{2} \; \rho \; L^2$$

so that the drag force becomes

$${\vec F}_{\rm drag} \; = \; - K(v) \; v^2 \; {\hat v} .$$ (2)

The functional dependence of K(v) can be obtained from the graphs or the approximate formula provided in Section 1.A, fit to specific data for the problem of interest, or simply approximated by some expression that allows one to solve the dynamical equations analytically.

My emphasis here will be on analytic solutions for the free-fall problem for forces with simple forms for K(v).

In one dimension (with ``down'' positive), the free fall of a body is due the the net force given by

$$F_{\rm net} \; = \; mg - K(v) \; v^2 .$$

We discuss the solution of this problem for certain special cases in the next section. Here we note that the speed when F_net vanishes is the terminal velocity, found by solving

$$mg \; = \; K(v) \; v^2$$

for v = V_max. (This is usually a non-linear equation, so the secant method or a graphical method would need to be used to find V_max.) Knowledge of V_max can be helpful when deciding if drag forces will be significant for the speeds typical in some situations.

Special cases that can be solved analytically - and which also make good approximations in certain real situations - are K(v) = K₁/v and K(v) = K₂. The first produces a drag force linear in v, typical for very low speeds or high viscosity (i.e. small Re), while the second produces a quadratic dependence on the speed as is commonly encountered for larger Re. Both of these situations can be seen in the C_D graphs in Section 1.A and are explained in Section 1.B.

Jump to Section 1.B:
Physical rationale for linear and quadratic drag regimes

Real objects

An object like a baseball, although essentially spherical, has surface defects (stitching) that make it different from the perfectly smooth sphere used for the measurements that produce the C_D graph in Section 1.A. Similarly, since we are interested in its behavior at quite large Reynolds numbers, the special case of the Stokes formula would not apply even if the ball were smooth. For most real objects, one has no choice but to use empirically determined parametrizations of the drag force or of K(v) or do a very sophisticated model calculation of the flow around the object. An example of data for drag forces on a baseball is given below.

Figure 1.3:

Graph, adapted from Ref. [2], of F_drag versus v
for a baseball (red curve) along with a linear
approximation (light blue curve) to those data.
The green circle shows the terminal velocity.

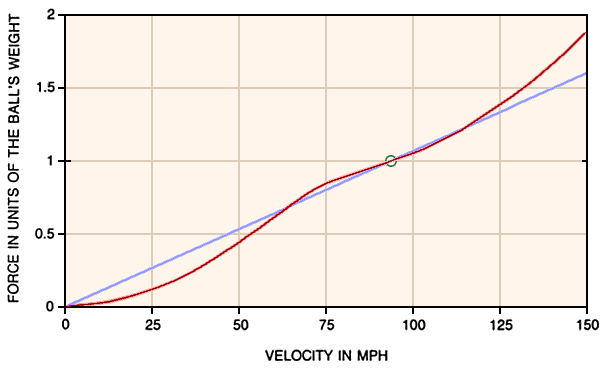
Note that F_drag is quadratic for low speeds and then goes through a transition region to a different quadratic dependence at high speeds. The region of most interest for the game of baseball happens to be where the forces are particularly complicated, and this is no accident -- it is due to the design of a ball that can be used to throw curves and other pitches between 70 and 100 mph. These data also tell us that numerical solutions are the only feasible approach to the analysis of baseball. If I did have to make analytic estimates, I would use the linear drag approximation that gives the correct terminal velocity, the light blue line shown in the figure.

Next, the General Solution for Simple Drag Parametrizations.