| (3) |
Back to the Introduction to Drag Forces.
The simplest parameterization of this problem takes the form of a
drag force that goes as a constant K times a power of the speed.
Assuming vertical free-fall, we can look at this in one dimension
where
It will prove convenient to rewrite this equation in terms of
some different constants.
With C = KN/m we get
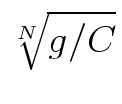 ,
which is
,
which is
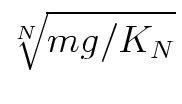 .
Integration of this equation will be much simpler if we rewrite it
by using aN = g/C.
This puts the problem in the form
.
Integration of this equation will be much simpler if we rewrite it
by using aN = g/C.
This puts the problem in the form
The differential equation in Eq. (4)
is solved by separation of variables. Some simple algebra gives
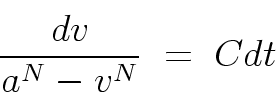
Note that the right hand side just gives C (t - t0) , which reduces to Ct with our initial conditions.
For the cases of interest, N=1 and N=2, the left hand side is easily integrated. (The case for N=3 can be integrated but I don't see how to write v(t) in a simple form. In any case, N=3 is not relevant to our focus on simple models.) Details for the linear and quadratic drag solutions are given in the next two sections.
Next, Linear (N=1 case) Drag.
Jim Carr