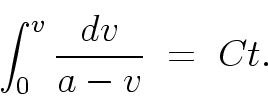Back to the General Solution for Simple Drag Parametrizations

3. Linear (N=1 case) Drag

The linear drag case has C = K₁/m and a = V_max = mg/K₁, so for free-fall from rest the integration problem is just

$$\int_{0}^{v} \frac{dv}{a - v} \; = \; C t .$$ (6)

With x = a - v, which is always positive, and dx = -dv, we identify the left side as a simple log integral:

$$\int_{0}^{v} \frac{dv}{a - v} \; = \; - \log(a-v) \biggr\vert_{0}^{v}$$

which gives

$$- \left[ \log(a-v) - \log(a) \right] \; = \; - \log\left(\frac{a-v}{a}\right)$$

so that Eq. (6) becomes

$$-Ct \; = \; \log\left(1 - \frac{v}{a}\right) .$$

Exponentiation of both sides gives

$$e^{-Ct} \; = \; 1 - \frac{v}{a}$$

so the solution for v(t) is

$$v(t) \; = \; V_{\rm max} \left[ 1 - e^{-Ct} \right]$$ (7)

where V_max = mg/K₁ and C is the inverse of the time constant for the exponential approach to the terminal velocity V_max. (Define T₁ = m/K₁ = 1/C to be that time constant.)

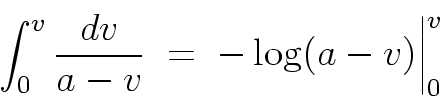
Similarly, if we assume that the initial position is y(0) = 0 and remember that the positive direction for y is down, we can integrate the velocity to get the position as a function of time:

$$y(t) \; = \; V_{\rm max} t \; - \; \left( \frac{V_{\rm max}}{C} \right) \left( 1 - e^{-Ct} \right)$$ (8)

This means that you would solve

$$H \; = \; V_{\rm max} T \; - \; \left( \frac{V_{\rm max}}{C} \right) \left( 1 - e^{-CT} \right)$$

for T to find out how long it takes for the object to fall a distance H.

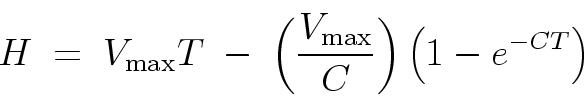
The validity of these solutions can be verified by explicit differentiation with respect to t and is left as an exercise.

Next, Quadratic (N=2 case) drag.