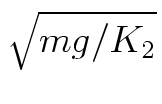 ,
so the integration problem becomes
,
so the integration problem becomes
Back to the N=1 (Linear Drag) case.
The more typical quadratic drag case has
C = K2/m
and a = Vmax =
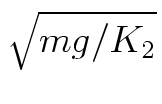 ,
so the integration problem becomes
,
so the integration problem becomes
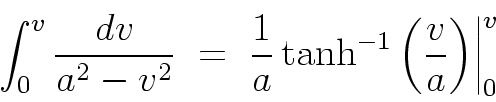
If we define B = aC =
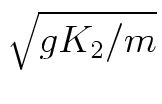 and take the tanh of
both sides of the equation, we can rewrite this as the solution for
v(t):
and take the tanh of
both sides of the equation, we can rewrite this as the solution for
v(t):
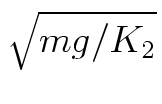 and we note that
B has the role of the inverse of a time constant in the
hyberbolic tangent function.
(Define T2 =
and we note that
B has the role of the inverse of a time constant in the
hyberbolic tangent function.
(Define T2 =
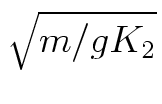 = 1/B as that time constant.)
= 1/B as that time constant.)
Further, if we assume that the initial position is y(0) = 0,
remember that the positive direction for y is down, and
integrate the velocity with respect to time, we get the result
The validity of this solution can be checked by explicit differentiation with respect to t and is left as an exercise.
Next, Sample Results.
Jim Carr